Exercice 1ere spécialité Maths - Probabilités, étude d'une fonction, inéquation

En lien avec la réforme du bac, découvre cet exercice en ligne, niveau 1ere spé maths, sur les probabilités, l'étude d'une fonction et la résolution d'une inéquation.

Ton prof de soutien scolaire en ligne te propose un sujet de bac 2021 corrigé destiné aux premières spécialités mathématiques.

Énoncé de cet exercice de maths

Lors d’une épidémie chez des bovins, on s’est aperçu que si la maladie est diagnostiquée suffisamment tôt chez un animal on peut le guérir, sinon la maladie est mortelle.
Un test est mis au point et essayé sur un échantillon d’animaux, la probabilité qu’il soit porteur de la maladie est x.
On obtient les résultats suivants :
Si un animal est porteur de la maladie, la probabilité que le test soit positif est égal à 0,7.
Si un animal est sain, la probabilité que le test soit négatif est égal à 0,9.
On choisit de prendre ces probabilités pour la population entière et d’utiliser le test pour un dépistage préventif de la maladie.
On note : M l’événement « l’animal est porteur de la maladie » T l’événement « le test est positif ».

Questions et corrigé

1. Construire un arbre pondéré modélisant la situation.

Réponse:

2. Exprimer en fonction de x la probabilité de l’événement T. Justifier.

Réponse :

Soit :

3. On note $P_{T}(M)$ la probabilité que l’animal soit malade sachant que son test est positif.Montrer que $P_{T}(M)=frac{7x}{6x+1})$ .

Réponse :

$P_{T}(M)=frac{P(Tcap M)}{P(T)}$ $P_{T}(M)=frac{0,7x}{0,6x+0,1}$

On multiplie par 10 numérateur et dénominateur, on obtient :

$P_{T}(M)=frac{7x}{6x+1}$

4. Soit f la fonction définie sur l’intervalle par $f(x)=frac{7x.}{6x+1}$

a) Etudier les variations de la fonction f.

Réponse :
Calculons la dérivée.
$f'(x)=frac{7(6x+1)-6(7x)}{(6x+1)^{2}}$ $f'(x)=frac{7}{(6x+1^{)2}}$ Donc 0" title="Rendered by QuickLaTeX.com" height="17" width="63" class="fr-fic fr-dii"> pour tout

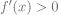
D’où le tableau de variation :

b) Tracer la courbe représentative (C ) de cette fonction.

Réponse :

c) Résoudre graphiquement l’inéquation .

Réponse:
On trouve : .

d) Vérifier par le calcul.

Réponse :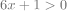
$frac{7x}{6x+1}geq0,9$ 0" title="Rendered by QuickLaTeX.com" height="13" width="72" class="fr-fic fr-dii"> donc Soit $xgeqfrac{0,9}{1,6}$ donc:.