Comment former et utiliser les superlatifs associés au present perfect en anglais ?
On a
De la relation on tire :
donc
est un parallélogramme
De la relation on tire :
donc :
et par conséquent :
est un rectangle (diagonales de même longueurs)
De la relation on tire :
donc
Par conséquent et
soit encore
et
perpendiculaires.
est un losange (diagonales perpendiculaires)
est parallélogramme, rectangle et losange donc
est un carré.
;
;
a) Formule: « =B3^2/($E$2*B2) »
b) Si alors
Si alors
a)
. Or,
Donc
est donc une suite arithmétique de 1er terme
et de raison
b) On a donc soit
4) a) Somme des termes d’ une suite arithmétique =
Donc soit
b) ;
etc.
donc
et
5) a) donc
soit
et donc
b) Algorithme :
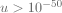 10^{-50}" width="67" height="15">
10^{-50}" width="67" height="15">
On trouve n=17
Avec une inéquation : on résout .
soit :
soit encore
On obtient : 
La plus petite valeur de n telle que est donc
Nombre de Fermat
1) a)
b) ;
;
; et
sont premiers, mais on ne peut pas en déduire que tous les nombres de Fermat sont premiers.
2) On en déduit que 641 est le 1er entier supérieur ou égal à 2 qui divise . Or

et donc
n’est pas premier.
Conclusion : les nombres de Fermat ne sont pas forcément premiers.
Pour tout 
On a donc
Montrons par récurrence la propriété :
Initialisation : Au rang on a
et
Hérédité : On suppose que pour 
Montrons qu’alors
Or, soit
L’hérédité est donc vérifiée.
Conclusion : La propriété est vraie pour et héréditaire, donc pour tout

.
D’après la question précédente U{2236}
Soit
Soit encore
Notons
On obtient
Conclusion : Pour tout entier naturel n et m tels que 
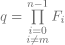
4) Soit deux entiers naturels tels et . D’après la question précédente il existe un entier naturel q tel que
.
D’après le Théorème de Bézout, 2 est un multiple du PGCD de .
Un nombre de Fermat est une puissance de 2 augmentée de 1, donc c’est un
nombre impair.
On en déduit que PGCD de pour tout couple d’entiers naturels
avec
Conclusion : 2 nombres de Fermat sont toujours premiers entre eux.
Comment former et utiliser les superlatifs associés au present perfect en anglais ?
Quelle est la différence entre "whether" et "if "?