Comment former et utiliser les superlatifs associés au present perfect en anglais ?
Déterminer la valeur approchée à 0,001 près de :
On partage [ a , b ] en n intervalles de même longueur
On considère les réels
On construit alors les rectangles de largeur h et de hauteur f(Xk), et les rectangles de largeur h et de hauteur f(Xk+1).
On note
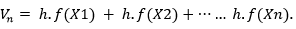
Si f est décroissante on a:
Si f est croissante on a:
Vn et Un sont des valeurs approchées de I.
 Programme Python
Programme PythonOn peut améliorer l’approximation en remplaçant les rectangles par des trapèzes comme le montre la figure ci-dessous :
Pour calculer l’aire du premier trapèze :
On fait ensuite un décalage de p pour calculer les aires des trapèzes suivants.
L’approximation de l’intégrale est alors :
On choisit au hasard un point M (x , y) en tirant de façon indépendante ses coordonnées x et y au hasard selon la loi uniforme sur [ 0 , 1 ].
On admet que la probabilité p qu’un point tiré de cette manière soit situé sous la courbe est égale à l’intégrale I.
En pratique, on initialise un compteur C à 0, on fixe un entier naturel n et on répète n fois le processus suivant :
On admet que f = C / n est une valeur approchée de I.
(Principe de la méthode dite de Monte Carlo)
Conclusion de cet exercice corrigé
|
Comment former et utiliser les superlatifs associés au present perfect en anglais ?
Quelle est la différence entre "whether" et "if "?