CRÉER UN COMPTE

Corrigé Bac Maths S Nouvelle Calédonie 2019 - Fonction Logarithme, Suites

Fonction Logarithme et suites au programme du bac maths de Nouvelle Calédonie 2019 dont nous te proposons un corrigé complet.

Dans ce cours de maths niveau lycée (terminale) ton prof de soutien scolaire en ligne revient sur le sujet de bac de Maths S donné en Nouvelle Calédonie en 2019

Sujet bac : fonction logarithme

Corrigé de cette épreuve de maths

Réponses:

$lim_{+infty}left(frac{3x+1}{x+1}right)=3$

Donc $lim_{+infty}f(x)=ln(3)$

Interprétation graphique: La droite d’équation est asymptote horizontale.

2)

a)

avec $U(x)=frac{3x+1}{x+1}$

soit $U'(x)=frac{3(x+1)-(3x+1)}{(x+1){{}^2}}=frac{2}{(x+1){{}^2}}$

$f'=frac{U'}{U}$

$f'(x)=frac{frac{2}{(x+1)text{texttwosuperior}}}{frac{3x+1}{x+1}}$

$f'(x)=frac{2}{(x+1){{}^2}}timesfrac{(x+1)}{(3x+1)}$

$f'(x)=frac{2}{(x+1)(3x+1)}$

b) 0" title="Rendered by QuickLaTeX.com" height="17" width="63" class="fr-fic fr-dii"> pour

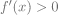
Donc f est strictement croissante sur

Énoncé du sujet : suite mathématique

Corrigé de cet exercice de bac

Réponses:

1)

Initialisation:
$U_{0}=3$ et $U_{1}=f(frac{5}{2})=ln2,5sim0,51$ On a donc: Donc $P_{0}$ vraie.

Hérédité:

Admettons $P_{n}$ vraie,

c’est à dire que: : $frac{1}{2}leq U_{n+1}leq U_{n}$

Montrons qu’alors $P_{n+1}$ vraie.

f est croissante donc si $frac{1}{2}leq U_{n+1}leq U_{n} alors f(frac{1}{2})leq f(U_{n+1})leq f(U_{n})$

Soit : $0,51leq U_{n+2}leq U_{n+1}$ et donc : $frac{1}{2}leq U_{n+2}leq U_{n+1}$

L’hérédité est bien vérifiée.

Conclusion: La propriété est héréditaire et vraie pour n=0; elle est donc vraie pour tout entier naturel.

On a donc: $frac{1}{2}leq U_{n+1}leq U_{n}$

2)

La suite est minorée et décroissante, elle est donc convergente.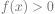
0" title="Rendered by QuickLaTeX.com" height="16" width="59" class="fr-fic fr-dii"> sur donc tous les termes de la suite sont strictement positifs.

Conclusion: La suite (Un) converge vers une limite strictement positive.

Partie C sujet bac Nouvelle Calédonie 2019

Réponses et corrigé

Réponses:

1)

Pour $xin[0;x_{0}]$ g est définie, continue et monotone.

Donc, d’après le corollaire du théorème des valeurs intermédiaires,

il n’existe pas $alphain[0;x_{0}]$ tel que .

Pour $in[x_{0;}+infty[$ g est définie, continue et monotone.

Donc, d’après le corollaire du théorème des valeurs intermédiaires,

il existe unique $in[x_{0};+infty[$ tel que .

Conclusion: L’équation g(x)=0 admet une unique solution strictement positive.

2)

a) Algorithme complété:

b)
Dernière valeur prise par la variable x lors de l’exécution de l’algorithme:

La calculatrice donne et .

donc x= 0,51

3)

soit .

Une valeur approchée à 0,01 près de la limite l de la suite (Un) est donc 0,51.

Superheroes, Superlatives & present perfect - Niveau Brevet

Comment former et utiliser les superlatifs associés au present perfect en anglais ?

Voir l'exercice

Condition et hypothèse en anglais

Quelle est la différence entre "whether" et "if "?

Voir l'exercice