Comment former et utiliser les superlatifs associés au present perfect en anglais ?
Note: Il peut y avoir plusieurs bonnes réponses.
| Questions | Réponse A | Réponse B | Réponse C | Réponse D |
| 1) Soit la suite |
La suite |
La suite |
La suite |
La suite |
| 2) Soit |
La suite |
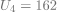 |
 |
La suite |
| 3) Soit |
La suite |
Pour tout n de N, |
 |
La suite |
| 4) La suite |
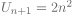 |
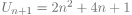 |
 |
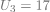 |
5) L’ensemble de définition de la fonction définie par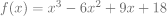 est : est : |
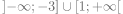 |
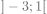 |
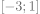 |
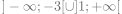 |
6) La fonction f définie sur ℝ par 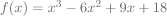 est : est : |
monotone sur ℝ. | croissante sur |
croissante sur |
strictement positive sur R. |
| 7) On considère la fonction f définie par |
f n’est ni définie, ni dérivable en 0. | f est définie, mais non dérivable en 0. | f est dérivable en 0, et f ‘(0)=0 |
La courbe représentant la fonction f, admet une tangente horizontale. |
| 8) On considère la fonction f définie par |
f est définie sur ℝ. | f est définie sur |
L’équation de la tangente T au point d’abscisse 0 est |
La tangente T est au-dessus de C sur ]0 ; 1 [ . |
| 9) Un professeur pose 3 questions sous forme de QCM avec 4 réponses possibles à chaque fois (dont une seule est exacte). Un élève répond au hasard à chaque question et indépendamment les unes des autres. La probabilité qu’il obtienne au moins une bonne réponse est égale à : | 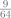 |
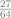 |
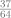 |
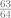 |
| 10) Dans un stand de tir, la probabilité pour un tireur d’atteindre la cible est de 0,3.On effectue n tirs consécutifs et indépendants. On désigne par |
6 | 7 | 12 | 14 |
Comment former et utiliser les superlatifs associés au present perfect en anglais ?
Quelle est la différence entre "whether" et "if "?