Comment former et utiliser les superlatifs associés au present perfect en anglais ?
Ton prof de soutien scolaire en ligne te propose un cours de maths complet niveau lycée (terminale) sur les suites et les algorithmes à partir d'un sujet de bac corrigé.
1.a) La diminution de revient à une multiplication par
soit par 0,96. On ajoute les 22 pommiers au résultat.
b) L’année 2020 correspond à l’indice n=2 (car 2020=2018+2). Nous pouvons calculer :
Arrondi à l’unité, le nombre de pommiers par hectare sera de 320.
2.a)
La valeur de N obtenue en sortie de l’algorithme sera l’indice de la première année pour laquelle le nombre de pommiers est strictement supérieur à 400.
b) La réalisation de l’algorithme donne en sortie N=13
3.a) Calculons le rapport de deux termes consécutifs défini si
Or,
est une suite géométrique de raison 0,96 et de premier terme
b)
c) En 2025, l’indice est 2025-2018=7
Le nombre de pommiers sera donc de : (arrondi à l’unité)
Arrondi à l’unité, le nombre de pommiers en 2025 sera donc de 5070
d) 
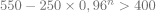

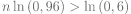

Le premier entier supérieur à cette valeur est n=13
Comment former et utiliser les superlatifs associés au present perfect en anglais ?
Quelle est la différence entre "whether" et "if "?