Utiliser les graphes probabilistes pour calculer des probabilités

A partir d'un exercice de bac corrigé, suis ce cours de soutien scolaire en ligne de maths niveau lycée sur les graphes probabilistes.

Énoncé (d'après un exercice de bac)

Deux chaines de télévision A et B programment chaque semaine, à la même heure, deux émissions concurrentes.

On suppose que le nombre global de téléspectateurs de ces émissions reste constant.

La 1ere semaine 70% de ces téléspectateurs ont regardé la chaîne A.

Une étude statistiques montre que :

15% des téléspectateurs qui ont regardé la chaîne A une semaine, regardent la chaîne B la semaine suivante.

10% des téléspectateurs qui ont regardé la chaîne B une semaine, regardent la chaîne A la semaine suivante.

On note respectivement a_n et b_n les proportions de téléspectateurs des chaînes A et B la nième semaine et P_n la matrice ligne ( a_n   b_n). On a donc par exemple P₁ = ( 0,7   0,3).

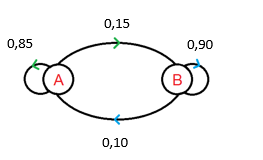
1a) Déterminer le graphe probabiliste représentant la situation.

1b) Donner la matrice de transition M associée à ce graphe.

2) Calculez M³ à l’aide de la calculatrice (Résultats arrondis à 10^-3 près).
Quelle est la répartition des téléspectateurs entre les deux chaînes lors de la 4eme semaine ?

3) On considère la matrice ligne P = (x   y) où x et y sont deux réels tels que x + y = 1

a) Déterminer x et y pour que

b) Interprétez les deux valeurs trouvées.

Corrigé de l'exercice

• 1) a) Graphe probabiliste représentant la situation:
• b) La matrice de transition de ce graphe probabiliste telle que pour tout entier naturel n non nul,  est :
• 2) Calculons M³
  
  Soit P₁ = (0,70   0,30) l'état probabiliste initial.
  L'état probabiliste de la 4ème semaine est : 
  Lors de la 4eme semaine, 53% des téléspectateurs regardent la chaîne A
  et 47% la chaîne B.
• 3 ) a)  Déterminons l'état stable du graphe probabiliste.
  Les termes de la matrice de transition M d'ordre 2 ne sont pas nuls, alors l'état probabiliste converge vers un état stable P= (x   y ) avec x + y = 1
  et vérifiant :
  
  L’état stable du système est donc : P = (0,40   0,60)  b) Interprétons le résultat obtenu dans le contexte de l'exercice :
  A partir d’un certain nombre de semaines, 40% des téléspectateurs regarderont la chaîne A et 60% la chaîne B.
  
  

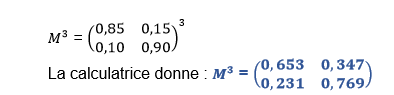
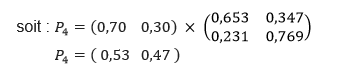
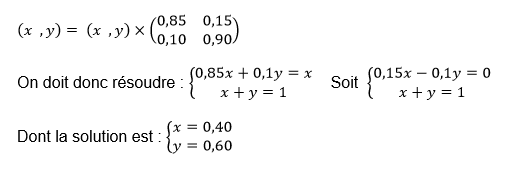
  Nos autres exercices corrigés sur les probabilités

  Calculer des probabilités avec la loi normale

  Calcul de probabilités avec la loi exponentielle

  Calculer des probabilités avec la loi uniforme