Corrigé maths Bac ES Nouvelle Calédonie 2018

Pour t’aider dans ton bac 2019, ton e-prof de soutien scolaire en ligne te propose ce corrigé de mathématiques du Bac ES Nouvelle Calédonie Novembre 2018.

$f^{prime }left( xright) =ln left( xright) +1$ donc réponse d

La courbe est concave puis convexe, réponse c.

Corrigé de ce sujet de bac 2018

La primitive de $fleft( xright) =3func{e}^{x}$ est $Fleft( xright) =3func{e}^{x}$ .

Donc $I=intlimits_{0}^{ln left( 2right) }3func{e}^{x}limfunc{d}% x=Fleft( ln left( 2right) right) -Fleft( 0right) =3func{e}^{ln left( 2right) }-3func{e}^{0}=3times 2-3times 1=3$ .

C’est donc la réponse a.

Les réponses a), b) et d) sont fausses donc la bonne réponse est c). On peut
le vérifier avec la calculatrice

$u_{2}=0,625times u_{1}+123=0,625times 490+123=429$

$u_{3}=0,625times u_{2}+123=0,625times 429+123=391$

Le nombre de demandeurs baisse de 37,5 % donc le nombre précédent de
demandeurs est multiplié par soit . Il faut ajouter au résultat 123 nouveaux demandeurs

Ceci donne : $u_{n+1}=0,625u_{n}+123.$

a) $v_{n}=u_{n}-328$

Donc $v_{n+1}=u_{n+1}-328=0,625u_{n}+123-328=0,625u_{n}-205$

Or $u_{n}=v_{n}+328$

On a donc : $v_{n+1}=0,625left( v_{n}+328right) -205=0,625v_{n}+205-205$

Soit $v_{n+1}=0,625v_{n}.$

$left( v_{n}right)$ est donc une suite géométrique de 1er terme $% v_{1}=U_{1}-328=490-328=162$ et de raison

b) On a donc $v_{n}=v_{1}times 0,625^{n-1}$ Soit $v_{n}=162times 0,625^{n-1}$

c) $u_{n}=v_{n}+328$

donc : $u_{n}=162times 0,625^{n-1}+328$

Calculer le nombre de demandeurs d’emploi au début du 2e trimestre 2019
revient à calculer
$u_{10}$

$u_{10}=162times 0,625^{9}+328=330$

Objectif à atteindre:

Or d’après la question précédente le nombre de demandeurs au début du 2eme
trimestre 2019 sera de 330.

Donc le directeur pourra atteindre son objectif.

A l’aide de la calculatrice on trouve $U_{7}=343.$

On peut aussi résoudre soit

soit

Soit encore frac{ln left( frac{15}{162}right) }{ln 0,625}" width="101" height="28">

5,1" width="79" height="14"> soit
6,1" width="52" height="14"> donc

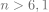
Donc l’objectif sera atteint au début du 3eme trimestre 2018.

1) Arbre de Probabilités

b) On utilise la loi des probabilités totales:

3) On doit calculer: $P_{R}(C)=frac{Pleft( Ccap Rright) }{P(R)}=frac{% 0,045}{0,159}=0,283$ Soit environ 28 %

Déterminons : la calculatrice donne

Ce résultat est cohérent avec la partie A ou on a trouvé ,avec définissant l’événement « Le trajet de l’employé a une durée inférieure à 30 minutes ».

Déterminons : la calculatrice donne

On en déduit 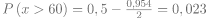60right) =0,5-frac{0,954}{2}=0,023" width="225" height="20">

a) Algorithme complété:

Tant que 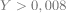0,008" width="72" height="14">

Fin Tant que

Après exécution de l’algorithme on obtient

Ceci signifie que la probabilité que la durée du trajet soit supérieure à 65
minutes est de 0,008.

1. Coût de production de 200 L de peinture: 3000 €.

2. Production de peinture pour une recette de 5000 € : 500 L

3. L’entreprise réalise un bénéfice à partir de 320 litres de peinture
vendus.

4. Le bénéfice correspond à l’écart entre les courbes recette et coût. L’écart maximal est de 2000 €. Donc l’entreprise ne peut pas réaliser un bénéfice de 3000 € pour une production variant entre 0 et 800 litres.

$f(8)=25times 8-150func{e}^{-5}=200-frac{150}{func{e}^{5}}$

$f^prime (x)=25+150times 0,5func{e}^{-0,5x+1}$

soit $f^prime (x)=25+75func{e}^{-0,5x+1}$

0" width="44" height="11"> ; 0" width="44" height="11"> et 0" width="84" height="14"> donc 0" width="63" height="17">

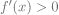
D’où le tableau de variation de f:

a) Pour , est définie, continue et monotone.

$left[ 150func{e};200-frac{150}{func{e}^{5}}right]$

$left[ -150func{e};200-frac{150}{func{e}^{5}}right]$

D’après le crollaire du théorème des valeurs intermédiaires, (TVI), il
existe unique appartenant à tel que

Avec la calculatrice on trouve (valeur arrondie au centième).

b) On en déduit que la quantité de peinture produite et vendue à partir de laquelle l’entreprise ECO-LOR réalisera un bénéfice est de 324 L ( Valeur arrondie au litre près)

a) ce graphe n’est pas complet car tous les sommets ne sont pas adjacents les uns avec les autres (par exemple, les sommets A et D ne sont pas adjacents car ils ne sont pas reliés par une arête).

b) ce graphe est connexe car pour chaque paire de sommets, il existe au moins une chaine les reliant, c’est ce que veut faire Naïma.

Ce graphe connexe admet une chaine eulérienne car les seuls sommets de degré impair sont le sommet E (degré 3) et le sommet S (degré 3) (le degré du sommet A est 2, le degré du sommet B est 4, le degré du sommet C est 2 et le degré du sommet D est 4).

En conclusion Naïma pourra exécuter sa mission.

Un trajet répondant à contrainte est par exemple E,B,S,D,B,C,D,E,A,S.

La matrice d’adjacence est $M=% begin{pmatrix} 0 & 1 & 1 & 0 & 1 & 0 \ 1 & 0 & 0 & 0 & 0 & 1 \ 1 & 0 & 0 & 1 & 1 & 1 \ 0 & 0 & 1 & 0 & 1 & 0 \ 1 & 0 & 1 & 1 & 0 & 1 \ 0 & 1 & 1 & 0 & 1 & 0% end{pmatrix}%$

a) Pour la première valeur manquante de la matrice $M^{2}$ , il faut multiplier la ligne 1 de la matrice par la colonne 4 de la matrice .On obtient alors :

Pour la deuxième valeur manquante de la matrice , il faut multiplier la ligne 4 de la matrice par la colonne 1 de la matrice . On obtient alors :

On aurait aussi pu effectuer , ce qui nous aurait permis de vérifier que est correcte.

b) Il suffit de regarder dans la matrice le coefficient de la ligne 1 (qui correspond au sommet ) et de la colonne 6 (qui correspond au sommet ). Sa valeur est 3.

On en déduit qu’il existe exactement 3 chemins qui utilisent deux pistes cyclables pour se rendre de l’école de musique à la salle de spectacle.

Algorithme de Dijkstra.

Le chemin le plus court est : E,B,D,S.

La durée, la plus courte, est donc de 8 minutes.

Corrigé maths Bac ES Nouvelle Calédonie 2018

MATIÈRES

Primaire

Français

Mathématiques

Collège

Anglais

Espagnol

Français

Géographie

Histoire

Italien

Mathématiques

Physique-Chimie

SVT

Révision Brevet

Lycée

Anglais

Espagnol

Français

Géographie

Histoire

Italien

Mathématiques

Philosophie

Physique-Chimie

SVT

Révision Bac

Pour t’aider dans ton bac 2019, ton e-prof de soutien scolaire en ligne te propose ce corrigé de mathématiques du Bac ES Nouvelle Calédonie Novembre 2018.

Corrigé de ce sujet de bac 2018