CRÉER UN COMPTE

Corrigé Bac ES Métropole 2019 - Etude graphique, fonction exponentielle, primitives, intégrales

Etude graphique, fonction exponentielle, primitives et intégrales au menu de ce corrigé de bac maths 2019.

A partir de cet exemple de sujet corrigé, ton prof de soutien scolaire en ligne te propose un cours de maths complet niveau lycée.

Énoncé de cet exercice de maths partie A

Corrigé de ce sujet de bac 2019

1)

2) A est un point d’inflexion donc

3) a)

b) On compte plus de 19 rectangles d’aire (On en compte environ 24)

Donc l’estimation de l’ébéniste semble incorrecte

Énoncé de ce sujet partie B

Corrigé de ce sujet sur une dérivée

Calcul de la dérivée

$f'(x)=14e^{-frac{x}{5}}-frac{1}{5}left(14x+42)right)e^{-frac{x}{5}}$

$f'(x)=frac{1}{5}left(70-14x-42)e^{-frac{x}{5}}right)$

$f'(x)=frac{1}{5}left(-14x+28)e^{-frac{x}{5}}right)$

2) a) 0,donc,f'(x),du,signe,de-14x+28,soit,du,signe,de,-x+2" title="Rendered by QuickLaTeX.com" class="fr-fic fr-dii" width="445" height="19">

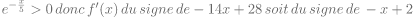
D’où le tableau du signe de f'(x)

b) Tableau de variation de f(x)

3) La 1ere ligne nous donne la forme développée de f ''(x), la seconde ligne sa forme factorisée.

0" title="Rendered by QuickLaTeX.com" class="fr-fic fr-dii" width="56" height="15"> donc .

donc f est concave sur ] et convexe sur

De plus la courbe représentant f admet un point d’inflexion pour

4) a) $G''(x)=-70e^{-frac{x}{5}}-frac{1}{5}left(-70x-560right)e^{-frac{x}{5}}$

$G''(x)=left(-70+14x+112right)e^{-frac{x}{5}}$

$G''(x)=left(14x+42right)e^{-frac{x}{5}}$

donc G est une primitive de g sur l’intervalle

b) On en déduit une primitive de f sur

$F(x)=70x+left(-70x-560right)e^{-frac{x}{5}}$

c) $smallint_{0}^{60}f(x)dx=F(60)-F(0)=4760-4760times e^{-12}$ unités d’aire.

$smallint_{0}^{60}f(x)dxsimeq4760$ unités d’aires

Surfaces à vernir : 4 faces plus le dossier

Soit: $4times4760+5400,simeq24440,cm{{}^2}$ Soit environ 2,444 m²

Or

Donc l’ébéniste devrait donc avoir suffisamment de vernis pour effectuer son travail.

Superheroes, Superlatives & present perfect - Niveau Brevet

Comment former et utiliser les superlatifs associés au present perfect en anglais ?

Voir l'exercice

Condition et hypothèse en anglais

Quelle est la différence entre "whether" et "if "?

Voir l'exercice